Supercharge Your Marketing: How CRM and Marketing Automation Work Together to Drive Growth

In the ever-evolving landscape of digital marketing, businesses are constantly seeking ways to streamline their operations, enhance customer engagement, and ultimately, boost their bottom line. One of the most effective strategies for achieving these goals is the integration of Customer Relationship Management (CRM) systems with marketing automation platforms. This powerful combination allows businesses to nurture leads, personalize customer experiences, and optimize their marketing efforts for maximum impact. This article delves into the intricacies of CRM for marketing automation, exploring its benefits, features, implementation strategies, and the future of this dynamic duo.
Understanding the Fundamentals: CRM and Marketing Automation Defined
Before diving into the synergy between CRM and marketing automation, it’s crucial to understand the individual roles of each component:
What is Customer Relationship Management (CRM)?
CRM is a technology that helps manage a company’s interactions with current and potential customers. At its core, a CRM system serves as a centralized database, storing customer information such as contact details, purchase history, communication logs, and more. This comprehensive view of each customer empowers businesses to:
- Improve Customer Service: By having all customer interactions in one place, support teams can quickly access information and provide personalized assistance.
- Enhance Sales Processes: Sales teams can use CRM data to identify leads, track opportunities, and manage the sales pipeline more efficiently.
- Gain Customer Insights: CRM systems provide valuable data on customer behavior, preferences, and needs, enabling businesses to make data-driven decisions.
- Foster Stronger Customer Relationships: By understanding customers better, businesses can build stronger, more meaningful relationships.
What is Marketing Automation?
Marketing automation involves using software to automate repetitive marketing tasks, improving efficiency and effectiveness. This can include:
- Email Marketing: Sending targeted email campaigns based on customer behavior and preferences.
- Social Media Marketing: Scheduling posts, monitoring social media activity, and engaging with followers.
- Lead Nurturing: Guiding potential customers through the sales funnel with automated email sequences and personalized content.
- Website Personalization: Tailoring website content and offers to individual visitors based on their browsing history and other data.
Marketing automation aims to streamline marketing processes, freeing up marketers to focus on more strategic initiatives and delivering more relevant experiences to customers.
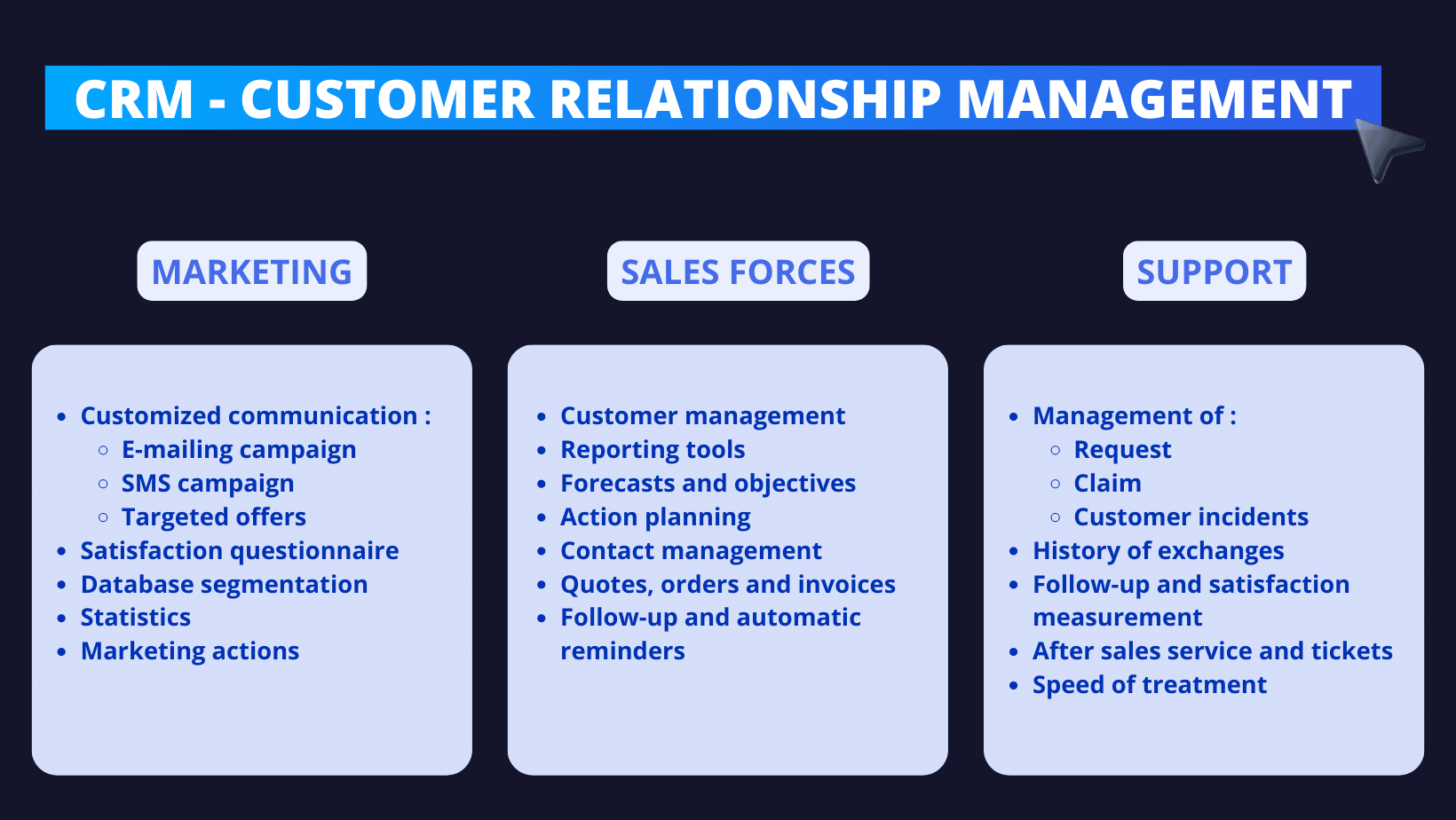
The Power of Integration: CRM for Marketing Automation
The true potential of CRM is unlocked when it’s integrated with marketing automation. This integration creates a powerful feedback loop, where data from the CRM system informs marketing automation activities, and data generated by marketing automation feeds back into the CRM. This synergy offers numerous advantages:
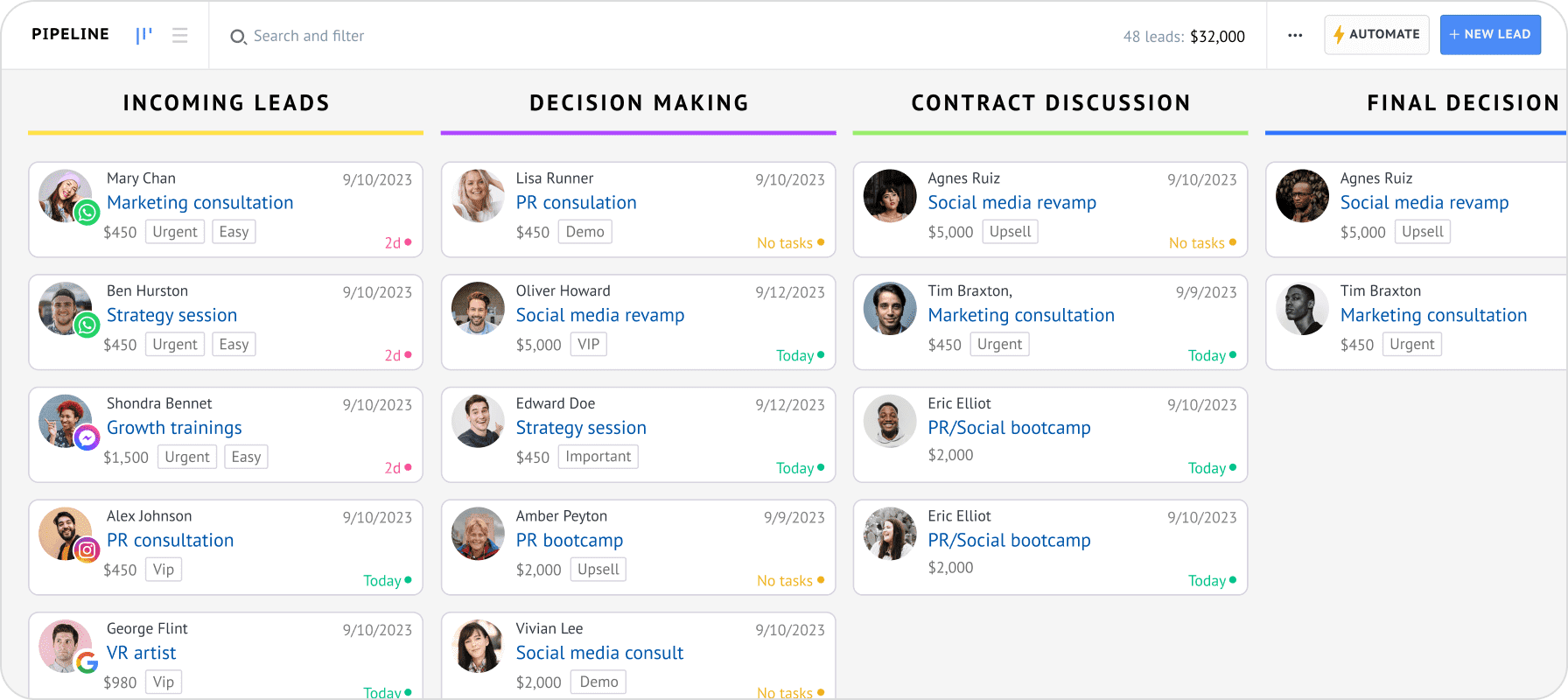
Improved Lead Management
CRM provides a centralized view of all leads, including their contact information, interactions, and lead scores. Marketing automation can then be used to nurture these leads with targeted content and campaigns, moving them through the sales funnel more effectively. For instance, a lead who downloads a specific ebook might be automatically added to a drip email campaign designed to educate them about your product or service.
Personalized Customer Experiences
With CRM and marketing automation working together, you can deliver highly personalized experiences to your customers. By leveraging customer data from the CRM, you can tailor your marketing messages, website content, and offers to individual customer preferences and behaviors. This level of personalization increases engagement, builds loyalty, and drives conversions.
Enhanced Marketing Efficiency
Marketing automation streamlines repetitive tasks, such as sending emails, scheduling social media posts, and segmenting your audience. This frees up your marketing team to focus on more strategic initiatives, such as developing new content, analyzing campaign performance, and optimizing your marketing strategy. The integration of CRM provides the data needed to make these optimizations more effective.
Better ROI on Marketing Spend
By targeting the right audience with the right message at the right time, CRM and marketing automation can significantly improve your return on investment (ROI). This is achieved through:
- Increased Conversion Rates: Personalized campaigns and targeted messaging are more likely to convert leads into customers.
- Reduced Marketing Waste: By focusing your efforts on the most promising leads, you can avoid wasting resources on those who are unlikely to convert.
- Improved Customer Retention: Personalized experiences and ongoing engagement build customer loyalty, leading to increased customer lifetime value.
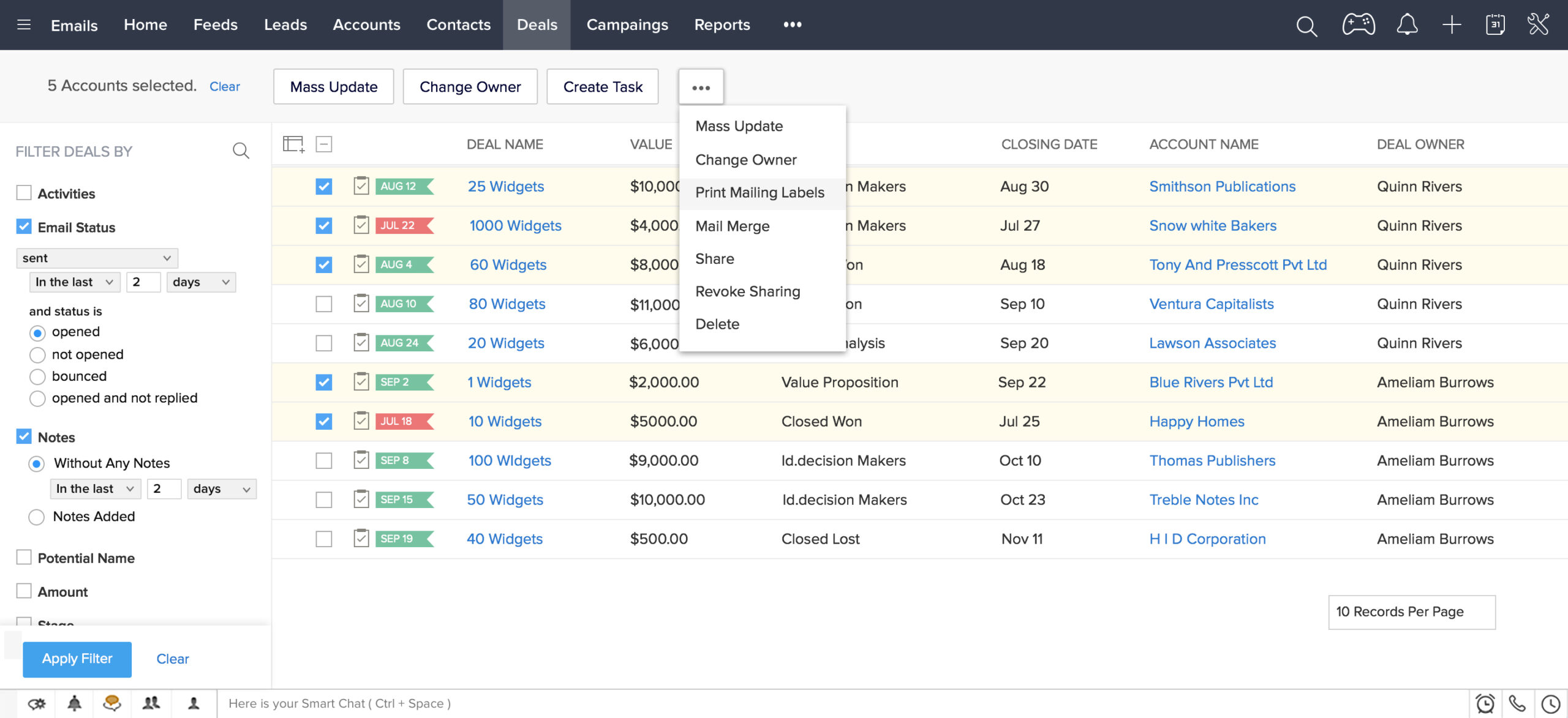
Key Features of a CRM for Marketing Automation
When selecting a CRM system for marketing automation, look for these essential features:
Contact Management
This is the foundation of any CRM, allowing you to store and manage customer contact information, including names, email addresses, phone numbers, and social media profiles.
Lead Management
The ability to track leads, assign lead scores, and manage the lead lifecycle is crucial for effective marketing automation. This includes features like lead scoring, lead nurturing workflows, and lead segmentation.
Email Marketing Integration
Seamless integration with email marketing platforms allows you to send targeted email campaigns, track open and click-through rates, and automate email workflows. This also includes features like A/B testing and email personalization.
Workflow Automation
Automation capabilities are at the heart of marketing automation. This allows you to create automated workflows for lead nurturing, customer onboarding, and other marketing activities. The best CRM systems offer a visual workflow builder that makes it easy to create and manage these workflows.
Segmentation
The ability to segment your audience based on various criteria, such as demographics, behavior, and purchase history, is essential for delivering targeted marketing messages. The CRM should allow you to create dynamic segments that automatically update as customer data changes.
Reporting and Analytics
Robust reporting and analytics features provide insights into campaign performance, customer behavior, and overall marketing effectiveness. This includes features like dashboards, custom reports, and the ability to track key metrics, such as conversion rates, ROI, and customer lifetime value.
Social Media Integration
Integration with social media platforms allows you to manage your social media presence, schedule posts, monitor social media activity, and engage with your audience. Some CRM systems also offer social listening capabilities, allowing you to track brand mentions and customer sentiment.
Integration with Other Tools
The CRM should integrate with other tools you use, such as your website, e-commerce platform, and other marketing tools. This ensures that data flows seamlessly between your systems, providing a holistic view of your customers.
Implementing CRM for Marketing Automation: A Step-by-Step Guide
Implementing a CRM for marketing automation can seem daunting, but following a structured approach can ensure a successful implementation:
1. Define Your Goals and Objectives
Before you start, clearly define your goals and objectives for using CRM and marketing automation. What do you want to achieve? Are you looking to increase leads, improve conversion rates, or enhance customer retention? Having clear goals will help you choose the right CRM system and develop an effective marketing strategy.
2. Choose the Right CRM System
There are numerous CRM systems available, each with its own strengths and weaknesses. Research different options and choose a system that meets your specific needs and budget. Consider factors such as:
- Features: Does the system offer the features you need, such as lead management, email marketing integration, and workflow automation?
- Scalability: Can the system scale to meet your future needs as your business grows?
- Ease of Use: Is the system user-friendly and easy to learn?
- Integration: Does the system integrate with other tools you use, such as your website, e-commerce platform, and other marketing tools?
- Pricing: Does the system fit within your budget?
3. Plan Your Implementation
Develop a detailed implementation plan that outlines the steps involved in setting up your CRM system and integrating it with your marketing automation platform. This plan should include:
- Data Migration: How will you migrate your existing customer data into the CRM system?
- System Configuration: How will you configure the CRM system to meet your specific needs?
- Workflow Design: How will you design and implement automated workflows for lead nurturing, customer onboarding, and other marketing activities?
- Training: How will you train your team to use the CRM system?
4. Migrate Your Data
Migrate your existing customer data into the CRM system. This process can be time-consuming, but it’s essential for ensuring that your CRM system has accurate and complete data. Clean your data and remove any duplicates or outdated information before migrating it.
5. Configure Your System
Configure the CRM system to meet your specific needs. This may include setting up custom fields, creating user roles, and integrating the system with other tools. Take the time to customize the system to your business processes and marketing strategy.
6. Integrate with Your Marketing Automation Platform
Integrate your CRM system with your marketing automation platform. This will allow you to share data between the two systems and automate marketing activities. The integration process will vary depending on the specific CRM system and marketing automation platform you are using.
7. Train Your Team
Train your team to use the CRM system and marketing automation platform. Provide them with the necessary training and resources to understand how to use the systems effectively. This will ensure that they can use the systems to their full potential and that the implementation is successful.
8. Launch Your Campaigns
Once your CRM system and marketing automation platform are set up and your team is trained, launch your marketing campaigns. Start with a pilot project to test your campaigns and make any necessary adjustments before rolling them out to a larger audience.
9. Monitor and Optimize
Continuously monitor your campaigns and analyze the results. Use the data from your CRM system and marketing automation platform to optimize your campaigns and improve your marketing strategy. Regularly review your processes and make adjustments as needed.
Choosing the Right CRM and Marketing Automation Tools
The market is saturated with CRM and marketing automation tools. The ideal choice depends on your business size, industry, and specific marketing requirements. Here’s a look at some popular options:
CRM Systems
- Salesforce: A leading CRM platform known for its robust features, customization options, and scalability. It’s a great choice for large enterprises.
- HubSpot CRM: A user-friendly CRM that’s free to start with and offers a comprehensive suite of marketing, sales, and service tools. Excellent for small to medium-sized businesses.
- Zoho CRM: A versatile CRM platform with a wide range of features and integrations, suitable for businesses of all sizes.
- Microsoft Dynamics 365: An integrated CRM and ERP solution that provides a comprehensive view of your business operations.
- Pipedrive: A sales-focused CRM designed to help sales teams manage their pipelines and close deals.
Marketing Automation Platforms
- HubSpot Marketing Hub: A complete marketing automation platform that integrates seamlessly with HubSpot CRM.
- Marketo (Adobe Marketo Engage): A powerful marketing automation platform designed for enterprise-level businesses.
- Pardot (Salesforce Pardot): A marketing automation platform specifically designed for B2B businesses.
- ActiveCampaign: A user-friendly platform that offers a wide range of marketing automation features, including email marketing, lead nurturing, and sales automation.
- Mailchimp: While primarily an email marketing platform, Mailchimp offers marketing automation features for small businesses and is easy to use.
When selecting tools, consider your budget, the complexity of your marketing needs, and the integration capabilities of each platform.
The Future of CRM for Marketing Automation
The future of CRM for marketing automation is bright, with several trends shaping its evolution:
Artificial Intelligence (AI) and Machine Learning (ML)
AI and ML are already transforming CRM and marketing automation. AI-powered chatbots provide instant customer support, ML algorithms analyze customer data to predict behavior, and AI-driven personalization delivers highly relevant experiences. Expect more AI-driven features in CRM and marketing automation tools in the future.
Hyper-Personalization
Customers expect personalized experiences, and CRM and marketing automation are evolving to meet this demand. Hyper-personalization involves tailoring marketing messages, content, and offers to individual customer preferences and behaviors, creating more engaging and effective interactions.
Omnichannel Marketing
Customers interact with businesses across multiple channels, including email, social media, website, and mobile apps. CRM and marketing automation are evolving to support omnichannel marketing, providing a seamless and consistent customer experience across all channels.
Increased Integration
Expect more integration between CRM systems and other marketing tools, such as social media management platforms, e-commerce platforms, and content management systems. This integration will provide a more holistic view of the customer and enable businesses to deliver more effective marketing campaigns.
Focus on Customer Experience
The customer experience is becoming increasingly important, and CRM and marketing automation are playing a key role in enhancing it. Businesses are using these tools to personalize customer interactions, provide exceptional customer service, and build lasting customer relationships.
Conclusion: Embracing the Power of CRM and Marketing Automation
The integration of CRM and marketing automation is a game-changer for businesses looking to improve their marketing efforts, enhance customer engagement, and drive growth. By leveraging the power of these two technologies, businesses can:
- Gain a 360-degree view of their customers.
- Personalize customer experiences.
- Automate repetitive marketing tasks.
- Improve lead management.
- Increase marketing efficiency.
- Achieve a better ROI on their marketing spend.
By carefully selecting the right tools, implementing them strategically, and continuously monitoring and optimizing their efforts, businesses can unlock the full potential of CRM for marketing automation and achieve their marketing goals. Embrace this powerful combination, and watch your marketing efforts transform into a well-oiled machine, driving growth and fostering lasting customer relationships. It’s not just about automating tasks; it’s about building meaningful connections, understanding your audience, and delivering value at every touchpoint.
The path to marketing success is paved with data, personalization, and automation. CRM and marketing automation are the compass and the engine that will get you there.