Level Up Your Marketing: How to Dominate with CRM, Webinars, and Hosting
In today’s fast-paced digital landscape, staying ahead of the curve in marketing is no longer a luxury; it’s a necessity. Businesses are constantly seeking innovative ways to connect with their target audience, nurture leads, and ultimately, drive conversions. This is where the powerful trio of Customer Relationship Management (CRM) software, webinar hosting, and robust website hosting comes into play. But it’s not just about having these tools; it’s about integrating them seamlessly to create a cohesive, data-driven marketing strategy.
This comprehensive guide will delve deep into the world of CRM marketing, webinar hosting, and the importance of reliable website hosting. We’ll explore how these three elements work in harmony to transform your marketing efforts, enabling you to build stronger customer relationships, generate high-quality leads, and boost your overall ROI. Whether you’re a seasoned marketer or just starting out, this article will provide you with actionable insights, practical tips, and real-world examples to help you master the art of integrated marketing.
The Power of CRM in Modern Marketing
At the heart of any successful marketing strategy lies a deep understanding of your customers. And that’s precisely where CRM software shines. CRM isn’t just a contact management system; it’s a powerful platform that allows you to centralize, analyze, and leverage customer data to create personalized experiences and drive engagement. Think of it as the central nervous system of your marketing efforts, providing you with the information and insights you need to make informed decisions.
What is CRM and Why Do You Need It?
CRM, or Customer Relationship Management, is a technology that helps businesses manage and analyze customer interactions and data throughout the customer lifecycle. It encompasses a wide range of functionalities, including contact management, lead tracking, sales automation, marketing automation, and customer service. The primary goal of CRM is to improve business relationships, retain customers, and drive sales growth.
In today’s competitive market, businesses need to go beyond basic contact information. They need to understand their customers’ preferences, behaviors, and needs. CRM provides the tools to achieve this by:
- Centralizing Customer Data: Consolidating all customer information in one place, providing a 360-degree view of each customer.
- Improving Communication: Facilitating personalized communication across various channels, such as email, phone, and social media.
- Automating Tasks: Automating repetitive tasks, such as lead scoring, email campaigns, and follow-up reminders, freeing up your team’s time.
- Enhancing Sales Performance: Providing sales teams with the tools they need to manage leads, track deals, and close more sales.
- Boosting Customer Satisfaction: Providing customer service teams with the information they need to resolve issues quickly and efficiently.
Key Features of Effective CRM Software
Not all CRM systems are created equal. To maximize the benefits of CRM, you need to choose a platform that offers the features you need to support your business goals. Some of the key features to look for include:
- Contact Management: Managing and organizing customer contacts, including their personal information, communication history, and interactions.
- Lead Management: Tracking and nurturing leads through the sales funnel, from initial contact to conversion.
- Sales Automation: Automating sales tasks, such as lead scoring, email campaigns, and follow-up reminders.
- Marketing Automation: Automating marketing tasks, such as email marketing, social media posting, and lead nurturing.
- Reporting and Analytics: Providing insights into your sales and marketing performance, allowing you to track key metrics and make data-driven decisions.
- Integration Capabilities: Integrating with other business tools, such as email marketing platforms, social media platforms, and e-commerce platforms.
- Mobile Accessibility: Allowing your team to access customer data and manage their sales and marketing activities from anywhere, at any time.
Choosing the Right CRM for Your Business
With a plethora of CRM solutions available, selecting the right one can feel overwhelming. Here are some factors to consider when making your decision:
- Business Needs: Identify your specific business needs and goals. What are you trying to achieve with CRM?
- Budget: Determine your budget and choose a CRM solution that fits your financial constraints.
- Scalability: Consider the scalability of the CRM platform. Will it be able to accommodate your business growth?
- Ease of Use: Choose a CRM platform that is user-friendly and easy to learn.
- Integration Capabilities: Ensure that the CRM platform integrates with your existing business tools.
- Customer Support: Look for a CRM provider that offers excellent customer support.
- Reviews and Ratings: Research and read reviews from other users to get an idea of the platform’s strengths and weaknesses.
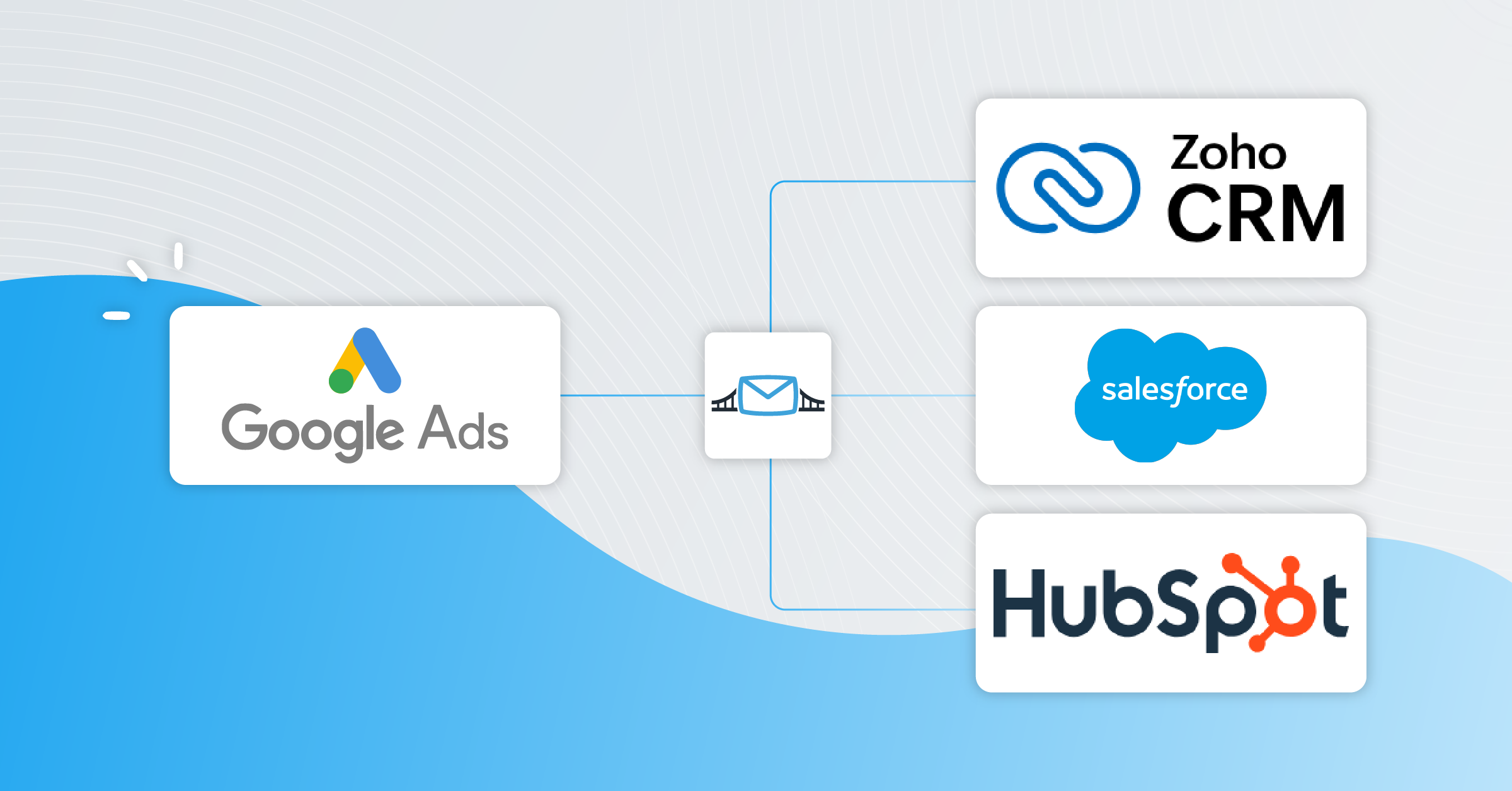
Popular CRM platforms include Salesforce, HubSpot, Zoho CRM, Microsoft Dynamics 365, and Pipedrive.
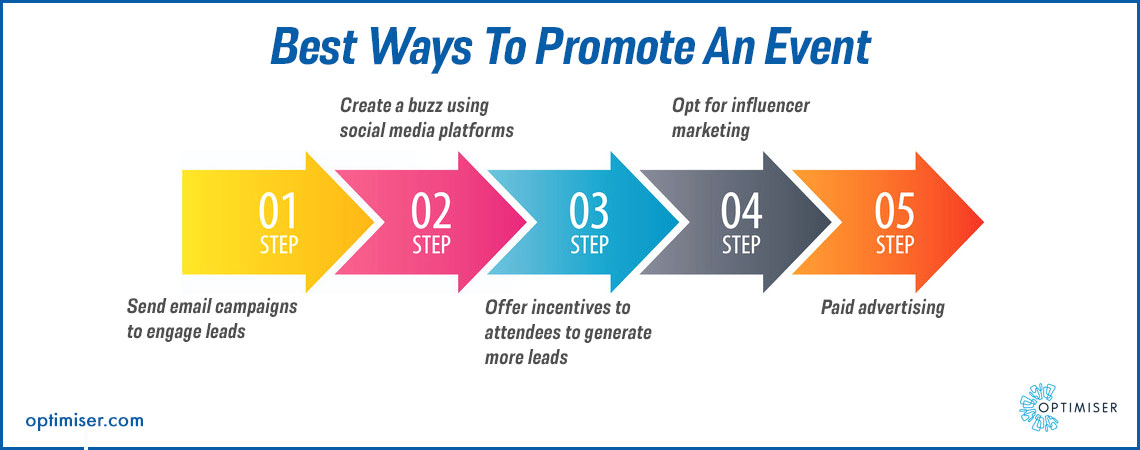
Webinars: The Ultimate Lead Generation Machine
Webinars have emerged as a powerful marketing tool, offering a unique opportunity to connect with your audience, establish thought leadership, and generate high-quality leads. They provide a platform for in-depth discussions, interactive presentations, and real-time engagement, making them a highly effective way to nurture leads and drive conversions. Webinars are more than just online presentations; they’re interactive experiences that can significantly impact your marketing ROI.
Why Webinars are Effective for Marketing
Webinars offer several advantages over traditional marketing methods:
- Lead Generation: Webinars are excellent lead magnets. By offering valuable content, you can attract potential customers and collect their contact information.
- Thought Leadership: Webinars allow you to showcase your expertise and establish yourself as a thought leader in your industry.
- Audience Engagement: Webinars provide an interactive platform for audience engagement, allowing you to answer questions, gather feedback, and build relationships.
- Brand Awareness: Webinars increase brand awareness and visibility by reaching a wider audience.
- Cost-Effectiveness: Webinars are a cost-effective marketing method, especially compared to in-person events.
- High Conversion Rates: Webinars often have higher conversion rates than other marketing methods because they allow you to build trust and credibility with your audience.
Planning and Hosting a Successful Webinar
To maximize the impact of your webinars, careful planning and execution are essential. Here’s a step-by-step guide to help you create successful webinars:
- Define Your Target Audience: Identify your ideal audience and tailor your content to their needs and interests.
- Choose a Compelling Topic: Select a topic that is relevant to your audience and addresses their pain points.
- Create High-Quality Content: Develop engaging and informative content that provides value to your audience.
- Select a Webinar Platform: Choose a reliable webinar platform that offers the features you need, such as screen sharing, chat, and Q&A functionality.
- Promote Your Webinar: Promote your webinar through various channels, such as email marketing, social media, and your website.
- Prepare Your Presentation: Create a visually appealing and well-structured presentation.
- Practice Your Presentation: Rehearse your presentation to ensure a smooth and engaging delivery.
- Engage with Your Audience: Interact with your audience during the webinar, answer their questions, and encourage their participation.
- Follow Up with Attendees: Send a follow-up email to attendees with a recording of the webinar, any resources mentioned, and a call to action.
Choosing the Right Webinar Hosting Platform
Selecting the right webinar hosting platform is crucial for a seamless and engaging webinar experience. Consider these factors when choosing a platform:
- Features: Look for features such as screen sharing, chat, Q&A functionality, polls, and recording capabilities.
- Ease of Use: Choose a platform that is user-friendly and easy to navigate.
- Reliability: Ensure the platform is reliable and can handle a large number of attendees without technical issues.
- Integration Capabilities: Check if the platform integrates with your CRM and other marketing tools.
- Pricing: Consider the pricing plans and choose a plan that fits your budget and needs.
- Customer Support: Look for a platform that offers excellent customer support.
Popular webinar hosting platforms include Zoom, GoToWebinar, WebinarJam, Demio, and Livestorm.
Website Hosting: The Foundation of Your Online Presence
Your website is your digital storefront, the primary hub for your online marketing efforts. And just like a physical storefront, it needs a solid foundation. That foundation is your website hosting. Choosing the right hosting provider is critical for website speed, security, and overall performance. It’s the unsung hero of your online marketing strategy, and its importance cannot be overstated.
Why Website Hosting Matters
Website hosting is the service that allows your website to be accessible on the internet. It provides the server space, bandwidth, and other resources necessary for your website to function properly. A reliable hosting provider ensures that your website is always available to your audience, loads quickly, and is protected from security threats. The quality of your hosting directly impacts user experience, search engine rankings, and ultimately, your bottom line.
- Website Speed: Fast loading times are essential for user experience and search engine optimization (SEO). A good hosting provider will provide the resources and infrastructure needed to ensure your website loads quickly.
- Website Security: Website security is paramount. A reliable hosting provider will implement security measures to protect your website from malware, hacking attempts, and other threats.
- Uptime: Uptime is the percentage of time your website is available to visitors. A high uptime rate is crucial for maintaining a positive user experience and avoiding lost sales.
- Scalability: As your website grows, you’ll need a hosting provider that can scale with your needs.
- Customer Support: Choose a hosting provider that offers excellent customer support to help you resolve any technical issues.
Types of Website Hosting
There are various types of website hosting available, each with its own advantages and disadvantages:
- Shared Hosting: This is the most affordable type of hosting, where your website shares server resources with other websites. It’s suitable for small websites with low traffic.
- VPS Hosting (Virtual Private Server): VPS hosting offers more resources and control than shared hosting. You get a dedicated portion of the server, providing better performance and security.
- Dedicated Hosting: With dedicated hosting, you have an entire server dedicated to your website. This offers the highest level of performance, security, and control, making it ideal for large websites with high traffic.
- Cloud Hosting: Cloud hosting utilizes a network of servers to host your website. It offers scalability, flexibility, and high availability.
Choosing the Right Website Hosting Provider
Selecting the right website hosting provider is a crucial decision. Here are some factors to consider:
- Performance: Look for a provider that offers fast loading times and high uptime.
- Security: Ensure the provider offers robust security measures to protect your website.
- Scalability: Choose a provider that can scale with your needs as your website grows.
- Customer Support: Look for a provider that offers excellent customer support.
- Pricing: Compare pricing plans and choose a plan that fits your budget.
- Reviews and Ratings: Research and read reviews from other users to get an idea of the provider’s strengths and weaknesses.
Popular website hosting providers include Bluehost, HostGator, SiteGround, WP Engine, and A2 Hosting.
Integrating CRM, Webinars, and Hosting for Marketing Success
The true power of CRM, webinars, and website hosting lies in their seamless integration. By combining these three elements, you can create a cohesive and data-driven marketing strategy that drives results. This integration allows you to streamline your marketing efforts, personalize customer experiences, and maximize your ROI. It’s about creating a synergistic approach where each element complements and enhances the others.
How to Integrate CRM with Webinars
Integrating your CRM with your webinar platform enables you to track leads, personalize communication, and measure the effectiveness of your webinars. Here’s how to do it:
- Capture Leads: Use your webinar platform to collect leads by integrating registration forms with your CRM.
- Track Attendee Data: Track attendee data, such as attendance, engagement, and questions asked, in your CRM.
- Segment Your Audience: Segment your audience based on their webinar attendance, engagement, and interests.
- Personalize Communication: Send personalized follow-up emails to attendees based on their webinar behavior.
- Nurture Leads: Use your CRM to nurture leads generated from your webinars with targeted email campaigns and other marketing activities.
- Measure ROI: Track the ROI of your webinars by measuring the number of leads generated, conversions, and revenue.
How to Integrate CRM with Your Website Hosting
Integrating your CRM with your website hosting allows you to personalize the user experience, track website activity, and improve lead generation. Here’s how:
- Implement Tracking Codes: Install tracking codes, such as Google Analytics and CRM tracking codes, on your website to track user behavior.
- Personalize Website Content: Personalize website content based on user data stored in your CRM.
- Create Dynamic Forms: Create dynamic forms that pre-populate with information from your CRM.
- Track Website Activity: Track website activity in your CRM to gain insights into customer behavior.
- Improve Lead Generation: Use your website to capture leads and integrate them with your CRM.
Best Practices for Integrated Marketing
To maximize the benefits of integrated marketing, follow these best practices:
- Define Your Goals: Clearly define your marketing goals and objectives.
- Choose the Right Tools: Select the right CRM, webinar platform, and website hosting provider for your business.
- Plan Your Strategy: Develop a comprehensive marketing strategy that integrates all three elements.
- Segment Your Audience: Segment your audience based on their behavior and interests.
- Personalize Your Communication: Personalize your communication based on customer data.
- Automate Your Tasks: Automate repetitive tasks, such as email campaigns and lead nurturing.
- Track Your Results: Track your results and make data-driven decisions.
- Continuously Optimize: Continuously optimize your marketing strategy based on your results.
Real-World Examples of Integrated Marketing Success
Let’s look at some real-world examples of how businesses are leveraging CRM, webinars, and website hosting to achieve marketing success:
- Example 1: Software Company: A software company uses its CRM to track leads generated from its webinars. They then segment the leads based on their engagement and send targeted email campaigns to nurture them through the sales funnel. The company also uses its website to host the webinar recordings and other resources, providing valuable content to its audience.
- Example 2: E-commerce Business: An e-commerce business uses its CRM to track customer data and personalize the shopping experience on its website. They also host webinars to showcase their products and drive sales. The business integrates its CRM with its webinar platform to track attendee data and send personalized follow-up emails with product recommendations.
- Example 3: Consulting Firm: A consulting firm uses its CRM to manage its client relationships and host webinars to generate leads. They integrate their CRM with their website to capture leads and track website activity. The firm also uses its website to provide valuable content and resources to its audience.
Conclusion: Embrace the Power of Integration
In conclusion, the integration of CRM, webinar hosting, and robust website hosting is a game-changer for modern marketing. By leveraging these three elements, businesses can build stronger customer relationships, generate high-quality leads, and boost their overall ROI. The power of this integrated approach lies in its ability to create a seamless, data-driven marketing experience that resonates with your target audience.
As you embark on your journey to transform your marketing efforts, remember to prioritize your customer, choose the right tools, and continuously optimize your strategy. The path to marketing success is paved with data, personalization, and a commitment to providing value. Embrace the power of integration, and watch your marketing efforts soar.
By following the strategies outlined in this comprehensive guide, you’ll be well-equipped to harness the power of CRM, webinars, and website hosting to achieve your marketing goals. Don’t just implement these tools; integrate them. This is where the true magic happens. Good luck, and happy marketing!