Zoho CRM Integration: Your Guide to Seamless Data Flow and Enhanced Customer Experiences

In today’s fast-paced business environment, the ability to seamlessly manage customer relationships is paramount. A Customer Relationship Management (CRM) system serves as the central nervous system of any customer-centric organization. It’s where you store vital information, track interactions, and nurture leads. However, the true potential of a CRM is unlocked when it’s integrated with other essential business tools. This is where Zoho CRM integration comes into play. This comprehensive guide delves into the world of Zoho CRM integration, exploring its benefits, how to implement it, and the various integrations available.

What is Zoho CRM?

Zoho CRM is a cloud-based CRM software designed to help businesses of all sizes manage their customer relationships, automate sales processes, and improve customer service. It’s a versatile platform offering a wide range of features, including:

Contact Management: Store and manage detailed customer information, including contact details, purchase history, and communication logs.
Lead Management: Track leads from initial contact to conversion, nurturing them through the sales pipeline.
Sales Automation: Automate repetitive sales tasks, such as email follow-ups and task assignments, freeing up your sales team to focus on closing deals.
Workflow Automation: Create automated workflows to streamline business processes and improve efficiency.
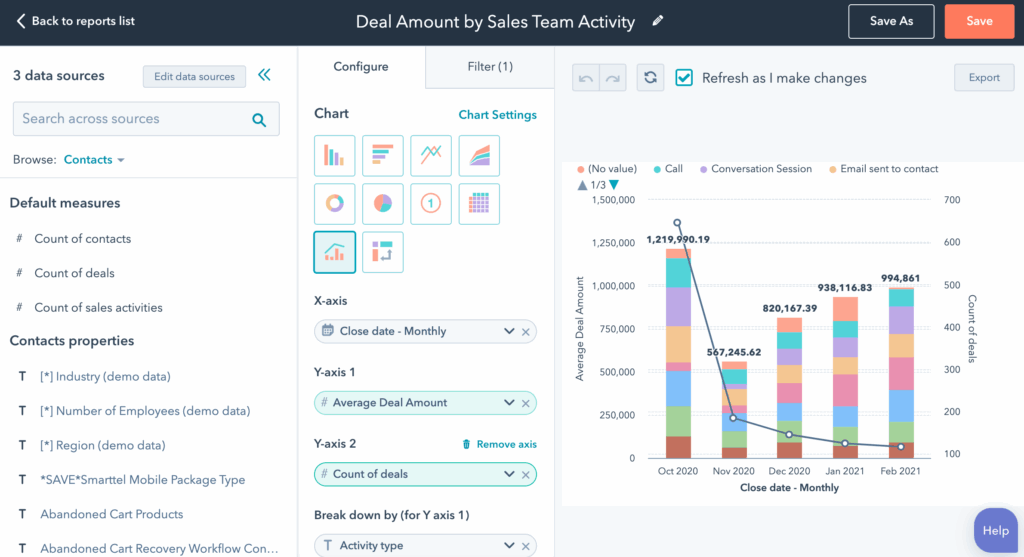
Reporting and Analytics: Generate insightful reports and dashboards to track key performance indicators (KPIs) and make data-driven decisions.
Customization: Tailor Zoho CRM to your specific business needs with custom fields, modules, and workflows.

The Importance of CRM Integration

Integrating your Zoho CRM with other applications is crucial for several reasons:

Data Consistency: Integration ensures that data is synchronized across all your systems, eliminating data silos and ensuring that everyone has access to the same, up-to-date information.
Improved Efficiency: By automating data entry and eliminating the need to switch between applications, integration streamlines workflows and saves valuable time.
Enhanced Productivity: Integrated systems enable your team to work more efficiently, allowing them to focus on higher-value tasks.
Better Decision-Making: With all your data in one place, you can gain a comprehensive view of your business and make more informed decisions.
Improved Customer Experience: Integrated systems enable you to provide a more personalized and consistent customer experience.

Benefits of Integrating Zoho CRM

Integrating Zoho CRM offers a plethora of benefits that can significantly impact your business’s performance:

Increased Sales: By automating sales processes and providing your sales team with access to the information they need, integration can help you close more deals and increase revenue.
Improved Customer Satisfaction: Integrated systems enable you to provide a more personalized and responsive customer service experience, leading to higher customer satisfaction.
Reduced Costs: By automating tasks and eliminating the need for manual data entry, integration can help you reduce operational costs.
Enhanced Collaboration: Integrated systems facilitate better collaboration between teams, ensuring that everyone is on the same page.
Better Data Accuracy: Integration minimizes the risk of data entry errors, ensuring that your data is accurate and reliable.

Popular Zoho CRM Integrations

Zoho CRM offers a wide range of integrations with popular business applications. Here are some of the most popular ones:

1. Email Marketing Platforms

Integrating Zoho CRM with email marketing platforms like Mailchimp, Constant Contact, and Campaign Monitor allows you to:

Sync Contact Data: Automatically sync contact information between your CRM and email marketing platform.
Segment Your Audience: Segment your audience based on CRM data, such as purchase history, lead source, and demographics.
Personalize Email Campaigns: Personalize your email campaigns with CRM data to improve engagement and conversions.
Track Campaign Performance: Track the performance of your email campaigns within Zoho CRM.

2. Accounting Software

Integrating Zoho CRM with accounting software like QuickBooks, Xero, and Zoho Books allows you to:

Automate Invoice Generation: Automatically generate invoices from within Zoho CRM.
Track Payments: Track payments and reconcile accounts.
Gain a 360-Degree View: Get a complete view of your customer’s financial history.

3. Help Desk Software

Integrating Zoho CRM with help desk software like Zendesk, Freshdesk, and Zoho Desk allows you to:

Track Customer Support Tickets: Track customer support tickets within Zoho CRM.
Provide Better Customer Service: Provide a more personalized and responsive customer service experience.
Improve Customer Satisfaction: Resolve customer issues quickly and efficiently.

4. Social Media Platforms

Integrating Zoho CRM with social media platforms like Facebook, Twitter, and LinkedIn allows you to:

Monitor Social Media Activity: Monitor social media activity related to your business.
Engage with Customers: Engage with customers on social media platforms.
Track Social Media Leads: Track leads generated from social media platforms.

5. Project Management Software

Integrating Zoho CRM with project management software like Asana, Trello, and Zoho Projects allows you to:

Manage Projects: Manage projects related to your customer relationships.
Track Project Progress: Track the progress of projects.
Improve Collaboration: Improve collaboration between teams.

6. Telephony Systems

Integrating Zoho CRM with telephony systems like RingCentral, Twilio, and 8×8 allows you to:

Make and Receive Calls: Make and receive calls directly from within Zoho CRM.
Log Call Details: Automatically log call details, such as call duration and call recordings.
Improve Sales Productivity: Improve sales productivity by automating call logging and other tasks.

How to Integrate Zoho CRM

Zoho CRM offers several ways to integrate with other applications:

1. Native Integrations

Zoho CRM has native integrations with many popular business applications. These integrations are pre-built and easy to set up. To use a native integration, simply go to the Zoho CRM Marketplace and select the application you want to integrate. Follow the on-screen instructions to connect the two applications.

2. Zoho Marketplace

Zoho Marketplace is a repository of pre-built integrations and extensions for Zoho CRM. Here, you can find integrations developed by Zoho and third-party developers. This is often the easiest way to connect to popular services.

3. APIs (Application Programming Interfaces)

Zoho CRM provides APIs that allow you to build custom integrations with other applications. This is a more advanced option, but it gives you the most flexibility. You’ll need to have some technical expertise to use the APIs.

4. Third-Party Integration Platforms

Third-party integration platforms, such as Zapier and Integromat, can connect Zoho CRM with thousands of other applications. These platforms offer a user-friendly interface and require no coding knowledge.

Step-by-Step Guide to Integrating with Zapier

Zapier is a popular integration platform that allows you to connect Zoho CRM with thousands of other apps. Here’s how to integrate Zoho CRM with Zapier:

Create a Zapier Account: If you don’t already have one, sign up for a Zapier account.
Connect Zoho CRM: Connect your Zoho CRM account to Zapier.
Choose a Trigger: Choose a trigger in Zoho CRM that will start the Zap. For example, you might choose “New Lead.”
Choose an Action: Choose an action in the other app that you want to perform. For example, you might choose “Create Contact” in Mailchimp.
Map Fields: Map the fields from Zoho CRM to the fields in the other app.
Test Your Zap: Test your Zap to make sure it’s working correctly.
Turn on Your Zap: Turn on your Zap to start automating your workflows.

Best Practices for Zoho CRM Integration

To ensure a successful Zoho CRM integration, follow these best practices:

Plan Your Integration: Before you start integrating, plan out your integration strategy. Identify the applications you want to integrate and the workflows you want to automate.
Choose the Right Integration Method: Choose the integration method that best suits your needs and technical expertise.
Test Your Integrations: Thoroughly test your integrations to ensure that they are working correctly.
Monitor Your Integrations: Monitor your integrations to ensure that they are running smoothly.
Keep Your Integrations Updated: Keep your integrations updated to ensure that they are compatible with the latest versions of the applications.
Security Considerations: Always prioritize security when integrating your CRM. Use secure connections and protect your data.
Data Mapping: Carefully map data fields between your applications to ensure accuracy and consistency.
User Training: Train your team on how to use the integrated systems to maximize their effectiveness.

Troubleshooting Common Integration Issues

Even with careful planning, you may encounter issues during the integration process. Here are some common problems and how to address them:

Data Synchronization Errors: Ensure that data fields are correctly mapped and that the integration has the necessary permissions.
Authentication Problems: Double-check your login credentials and API keys.
Workflow Issues: Review your workflows and triggers to identify any potential problems.
Performance Issues: Optimize your integration settings and consider the impact on system performance.
API Limits: Be aware of API rate limits imposed by the integrated applications.

Advanced Zoho CRM Integration Strategies

Once you’ve mastered the basics, you can explore more advanced integration strategies:

Custom Integrations: Develop custom integrations using APIs to meet specific business needs.
Data Warehousing: Integrate Zoho CRM with a data warehouse to create comprehensive reports and analyses.
AI-Powered Integrations: Leverage AI to automate tasks and gain deeper insights from your customer data.
Multi-Platform Integration: If you use multiple Zoho products, integrate them for a seamless user experience.

Zoho CRM Integration: A Real-World Example

Let’s consider a hypothetical scenario. A small e-commerce business, “GlowUp Gadgets,” uses Zoho CRM to manage its customer relationships and Mailchimp for email marketing. They want to integrate the two systems to automatically add new leads from Zoho CRM to a specific Mailchimp audience and track email campaign performance within their CRM.

Here’s how they could achieve this using Zapier:

Trigger: Set up a trigger in Zapier that activates when a new lead is created in Zoho CRM.
Action: Configure the action to add the new lead to a specific Mailchimp audience. Map the relevant fields from Zoho CRM (e.g., name, email address) to the corresponding fields in Mailchimp.
Testing: Test the Zap to ensure that new leads are automatically added to the Mailchimp audience.
Tracking: Set up tracking within Zoho CRM to monitor the performance of email campaigns sent through Mailchimp. This could involve tracking email opens, clicks, and conversions, providing valuable insights into customer engagement and sales effectiveness.

With this integration, GlowUp Gadgets can:

Automate lead nurturing: Automatically add new leads to their email marketing campaigns.
Improve customer engagement: Send targeted email campaigns based on customer data stored in Zoho CRM.
Measure campaign effectiveness: Track the performance of their email campaigns within Zoho CRM.

The Future of Zoho CRM Integration

The future of Zoho CRM integration is bright, with exciting developments on the horizon:

AI-Powered Integrations: Expect to see more AI-powered integrations that automate tasks, provide insights, and personalize customer experiences.
No-Code Integration Platforms: No-code integration platforms will continue to evolve, making it easier for businesses of all sizes to connect their applications.
Deeper Integrations: Integrations will become more sophisticated, providing a more seamless and comprehensive experience.
Focus on Data Security: Data security will remain a top priority, with integrations incorporating advanced security features.

Conclusion

Zoho CRM integration is a powerful tool that can transform your business. By integrating your CRM with other applications, you can streamline workflows, improve efficiency, enhance productivity, and deliver a better customer experience. Whether you’re a small business or a large enterprise, Zoho CRM integration can help you achieve your business goals. By understanding the benefits, implementation methods, and best practices, you can unlock the full potential of Zoho CRM and take your customer relationships to the next level.

Embrace the power of seamless data flow. Integrate your Zoho CRM today and embark on a journey of enhanced customer experiences and business growth!

Zoho CRM Integration: Unleashing the Power of Seamless Data Flow and Enhanced Customer Experiences