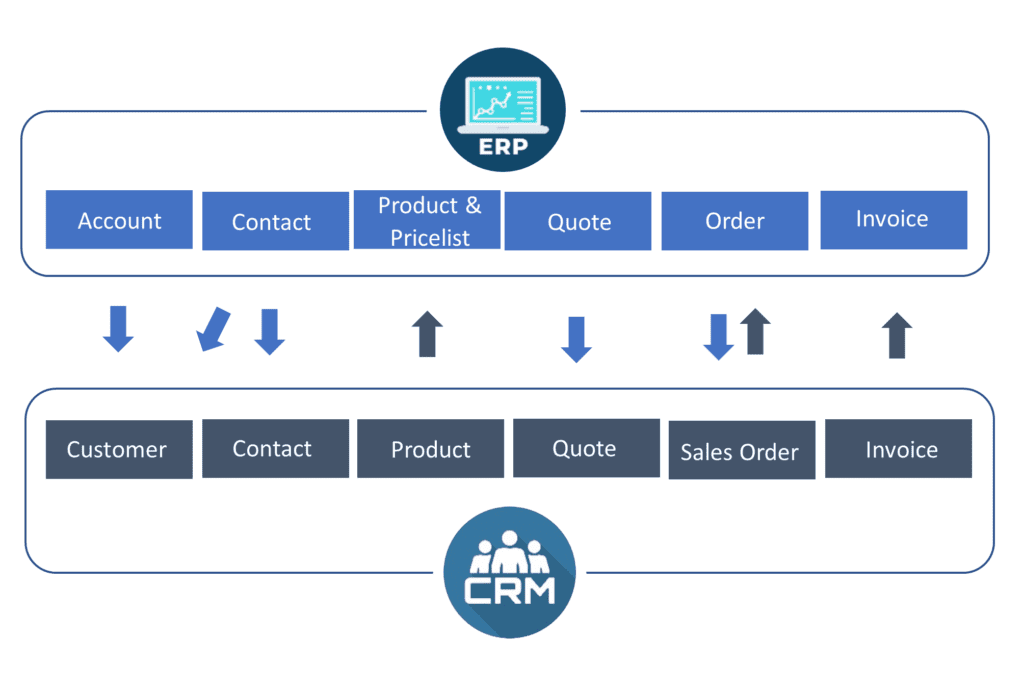
Introduction: The Power of CRM in Modern Marketing
In today’s hyper-competitive business landscape, understanding and nurturing customer relationships is no longer a luxury; it’s a necessity. Customer Relationship Management (CRM) systems have emerged as the cornerstone of this approach, providing businesses with the tools they need to streamline interactions, personalize experiences, and ultimately, drive revenue growth. This article dives deep into CRM marketing success stories, illustrating how companies across various industries have leveraged the power of CRM to achieve remarkable results. We’ll explore real-world examples, analyze the strategies employed, and uncover the key takeaways that can inspire your own CRM journey.
What is CRM Marketing? A Brief Overview
Before we delve into the success stories, let’s briefly define CRM marketing. It’s a strategic approach that centers on using CRM systems to manage and analyze customer data throughout the customer lifecycle. This involves:
- Data Collection: Gathering information about customers, including their demographics, purchase history, preferences, and interactions.
- Segmentation: Grouping customers based on shared characteristics to tailor marketing messages.
- Personalization: Delivering customized content and offers that resonate with individual customer needs.
- Automation: Automating repetitive tasks, such as email marketing and lead nurturing, to improve efficiency.
- Analysis: Tracking key performance indicators (KPIs) to measure the effectiveness of marketing campaigns and identify areas for improvement.
The ultimate goal of CRM marketing is to build lasting customer relationships, increase customer loyalty, and boost profitability.
Success Story 1: Salesforce and the Transformation of a Retail Giant
Let’s start with a classic: Salesforce. While Salesforce is a CRM platform itself, many businesses have built their success stories *on* Salesforce. Consider the case of a major retail chain, let’s call them “MegaMart.” Before implementing Salesforce, MegaMart struggled with fragmented customer data. Information was scattered across various departments, making it difficult to gain a holistic view of each customer. Marketing campaigns were often generic and ineffective, leading to low conversion rates and customer churn.
The Challenge: Disconnected customer data, generic marketing, and high customer churn.
The Solution: MegaMart implemented Salesforce to centralize customer data, enabling a 360-degree view of each customer. They integrated data from various sources, including point-of-sale systems, online interactions, and customer service interactions. This unified view allowed them to segment customers based on their purchase history, demographics, and preferences. They then used Salesforce’s marketing automation capabilities to create personalized email campaigns, targeted product recommendations, and customized offers. Furthermore, the sales team gained a better understanding of each customer’s needs, leading to more effective sales interactions.
The Results:
- Increased Sales: Personalized marketing campaigns led to a significant increase in sales and revenue.
- Improved Customer Retention: By understanding customer needs and providing personalized experiences, MegaMart reduced customer churn.
- Enhanced Customer Satisfaction: Customers felt valued and understood, leading to higher satisfaction scores.
- Improved Marketing ROI: Targeted campaigns generated a better return on investment compared to generic marketing efforts.
Key Takeaway: Centralizing customer data and leveraging personalization are crucial for driving sales and improving customer retention. Salesforce, and other robust CRM platforms, can be instrumental in achieving these goals.
Success Story 2: HubSpot and the Growth of a SaaS Startup
Moving on to a different type of business, let’s examine how HubSpot helped a Software as a Service (SaaS) startup, “InnovateTech,” scale its operations. InnovateTech was a young company with a promising product but a limited marketing budget. They needed a CRM solution that was affordable, easy to use, and capable of supporting their growth ambitions. HubSpot proved to be the perfect fit.
The Challenge: Limited marketing budget, need for an all-in-one solution, and rapid growth expectations.
The Solution: InnovateTech adopted HubSpot’s CRM platform, which offered a suite of marketing, sales, and customer service tools. They used HubSpot to:
- Attract Leads: Create engaging content, optimize their website for search engines, and run targeted social media campaigns.
- Nurture Leads: Automate email marketing campaigns to nurture leads through the sales funnel.
- Close Deals: Manage sales pipelines, track deals, and improve sales team efficiency.
- Provide Customer Service: Manage customer inquiries and provide support through a centralized platform.
The Results:
- Increased Lead Generation: HubSpot’s marketing tools helped InnovateTech attract a large volume of qualified leads.
- Improved Sales Conversion Rates: By streamlining the sales process, InnovateTech increased its sales conversion rates.
- Reduced Customer Acquisition Cost: HubSpot’s inbound marketing strategies helped InnovateTech reduce its customer acquisition cost.
- Scalable Growth: HubSpot’s platform supported InnovateTech’s rapid growth, allowing them to expand their customer base and revenue.
Key Takeaway: For startups and small businesses, an all-in-one CRM platform like HubSpot can be a cost-effective and powerful solution for driving growth and improving efficiency.
Success Story 3: Zendesk and Revolutionizing Customer Support
Let’s shift our focus to customer service. Consider “GlobalTech,” a multinational company with a large customer base and a complex support infrastructure. Before implementing Zendesk, GlobalTech’s customer support was fragmented and inefficient. Customers often had to wait long periods for responses, and support agents lacked access to the necessary information to resolve issues quickly. This led to frustration and a decline in customer satisfaction.
The Challenge: Fragmented customer support, long response times, and declining customer satisfaction.
The Solution: GlobalTech deployed Zendesk to centralize its customer support operations. Zendesk provided a unified platform for managing customer inquiries, tracking issues, and providing support across multiple channels, including email, phone, and live chat. GlobalTech implemented:
- Help Desk: A centralized help desk to manage customer tickets and track issue resolution.
- Knowledge Base: A self-service knowledge base to empower customers to find answers to their questions.
- Live Chat: Live chat functionality to provide instant support to customers.
- Reporting and Analytics: Reporting and analytics tools to track key performance indicators (KPIs) and identify areas for improvement.
The Results:
- Reduced Response Times: Zendesk helped GlobalTech significantly reduce its customer response times.
- Improved Customer Satisfaction: Customers were happier with the faster and more efficient support they received.
- Increased Agent Productivity: Zendesk streamlined the support process, increasing agent productivity.
- Cost Savings: By improving efficiency, GlobalTech reduced its customer support costs.
Key Takeaway: A robust CRM system like Zendesk can revolutionize customer support by providing a centralized platform for managing inquiries, empowering customers with self-service options, and improving agent efficiency.
Success Story 4: Mailchimp and the Power of Email Marketing Automation
While Mailchimp is primarily an email marketing platform, it also integrates with many CRM systems, allowing businesses to automate their email marketing efforts based on CRM data. Consider “LocalBrew,” a local craft brewery that wanted to increase customer engagement and drive sales. They were already using a CRM to track customer data, but their email marketing was limited and manual.
The Challenge: Limited email marketing, manual processes, and need for increased customer engagement.
The Solution: LocalBrew integrated Mailchimp with their existing CRM system. They used Mailchimp to:
- Segment Customers: Segment customers based on their purchase history, location, and preferences.
- Automate Email Campaigns: Automate email campaigns, such as welcome emails, birthday emails, and promotional offers.
- Personalize Emails: Personalize emails based on customer data, such as their name and purchase history.
- Track Campaign Performance: Track email campaign performance and make data-driven decisions.
The Results:
- Increased Customer Engagement: Automated and personalized email campaigns increased customer engagement.
- Improved Sales: Targeted email campaigns drove sales and revenue.
- Enhanced Customer Loyalty: Customers felt valued and connected to the brand.
- Time Savings: Automated email campaigns saved LocalBrew time and resources.
Key Takeaway: Integrating an email marketing platform like Mailchimp with your CRM system can significantly enhance your email marketing efforts and drive customer engagement.
Success Story 5: Oracle Siebel and Enterprise-Level CRM Transformation
For large enterprises, Oracle Siebel CRM offers a comprehensive solution for managing complex customer relationships. Consider “GlobalCorp,” a multinational corporation with a complex sales process and a need for a robust CRM system to manage its extensive customer base. Before implementing Siebel, GlobalCorp struggled with fragmented sales data, inefficient sales processes, and a lack of visibility into the sales pipeline.
The Challenge: Fragmented sales data, inefficient sales processes, and lack of sales pipeline visibility.
The Solution: GlobalCorp deployed Oracle Siebel CRM to centralize sales data, automate sales processes, and improve sales pipeline visibility. They implemented:
- Sales Force Automation: Automate sales tasks, such as lead management, opportunity management, and quote generation.
- Sales Analytics: Provide sales teams with real-time insights into sales performance.
- Customer Service: Integrate customer service functions to provide a seamless customer experience.
- Partner Relationship Management: Manage relationships with channel partners.
The Results:
- Improved Sales Productivity: Siebel streamlined sales processes, increasing sales productivity.
- Increased Sales Revenue: Improved sales pipeline visibility and sales automation led to a significant increase in sales revenue.
- Enhanced Customer Satisfaction: A seamless customer experience improved customer satisfaction.
- Better Decision-Making: Real-time sales analytics enabled better decision-making.
Key Takeaway: For large enterprises, a comprehensive CRM solution like Oracle Siebel can transform sales operations, improve customer relationships, and drive revenue growth.
Key Strategies for CRM Marketing Success
These success stories highlight the diverse ways businesses can leverage CRM to achieve their marketing goals. However, the specific strategies employed will vary depending on the business, its industry, and its target audience. Here are some key strategies that underpin successful CRM marketing initiatives:
- Data-Driven Personalization: Use customer data to personalize marketing messages, offers, and experiences.
- Customer Segmentation: Divide your customer base into segments based on shared characteristics to tailor your marketing efforts.
- Marketing Automation: Automate repetitive tasks, such as email marketing and lead nurturing, to improve efficiency and save time.
- Omnichannel Approach: Provide a consistent customer experience across all channels, including email, phone, social media, and in-person interactions.
- Lead Scoring: Prioritize leads based on their likelihood to convert and focus your sales efforts on the most promising prospects.
- Customer Journey Mapping: Map the customer journey to understand how customers interact with your business and identify opportunities to improve their experience.
- Integration: Integrate your CRM system with other business systems, such as your website, e-commerce platform, and social media channels.
- Continuous Improvement: Regularly analyze your CRM data and marketing campaigns to identify areas for improvement and optimize your strategies.
Choosing the Right CRM System
Selecting the right CRM system is a critical decision that can significantly impact the success of your CRM marketing efforts. Here are some factors to consider when choosing a CRM system:
- Business Needs: Identify your specific business needs and requirements. Consider the size of your business, your industry, and your marketing goals.
- Features and Functionality: Evaluate the features and functionality offered by different CRM systems. Make sure the system has the features you need, such as contact management, lead management, sales force automation, marketing automation, and customer service.
- Scalability: Choose a CRM system that can scale to meet your future growth needs.
- Integration: Ensure the CRM system integrates with your existing business systems, such as your website, e-commerce platform, and email marketing platform.
- Ease of Use: Choose a CRM system that is easy to use and understand. Training should be readily available.
- Cost: Consider the cost of the CRM system, including the initial setup costs, ongoing subscription fees, and any additional costs for training or support.
- Vendor Reputation: Research the vendor’s reputation and read reviews from other users.
- Security: Ensure the CRM system has robust security features to protect your customer data.
Some popular CRM systems include:
- Salesforce
- HubSpot
- Zoho CRM
- Microsoft Dynamics 365
- Pipedrive
- Zendesk
Measuring CRM Marketing Success: Key Metrics
To gauge the effectiveness of your CRM marketing efforts, it’s crucial to track key performance indicators (KPIs). Here are some essential metrics to monitor:
- Customer Acquisition Cost (CAC): The cost of acquiring a new customer.
- Customer Lifetime Value (CLTV): The predicted revenue a customer will generate over their relationship with your business.
- Conversion Rates: The percentage of leads that convert into customers.
- Customer Retention Rate: The percentage of customers who remain customers over a given period.
- Customer Churn Rate: The percentage of customers who stop doing business with your company.
- Website Traffic: The number of visitors to your website.
- Lead Generation: The number of leads generated through your marketing efforts.
- Sales Revenue: The total revenue generated from sales.
- Marketing ROI: The return on investment for your marketing campaigns.
- Customer Satisfaction (CSAT) Score: Measures customer satisfaction.
- Net Promoter Score (NPS): Measures customer loyalty.
Regularly analyzing these metrics will provide valuable insights into the performance of your CRM marketing initiatives and help you identify areas for improvement.
Challenges and Pitfalls to Avoid
While CRM offers significant benefits, implementing and managing a CRM system can be challenging. Here are some common pitfalls to avoid:
- Poor Data Quality: Inaccurate or incomplete data can undermine the effectiveness of your CRM efforts.
- Lack of User Adoption: If employees don’t use the CRM system, it won’t be effective.
- Poor Integration: If the CRM system doesn’t integrate with your other business systems, it can create data silos and inefficiencies.
- Lack of Training: Without proper training, employees may not know how to use the CRM system effectively.
- Unrealistic Expectations: Don’t expect immediate results. CRM implementation takes time and effort.
- Ignoring Customer Feedback: Actively solicit customer feedback and use it to improve your CRM efforts.
- Focusing on Technology Over Strategy: The CRM system is a tool, not a strategy. You need a clear CRM strategy to be successful.
Conclusion: Embracing the Future of Customer Relationships
CRM marketing is no longer optional; it’s a core component of any successful business strategy. The success stories we’ve explored demonstrate the transformative power of CRM in driving sales, improving customer satisfaction, and fostering lasting customer relationships. By understanding the key strategies, choosing the right CRM system, and measuring your results, you can unlock the full potential of CRM marketing and propel your business to new heights. Embrace the future of customer relationships and embark on your own CRM journey today.
Remember, the most successful CRM initiatives are those that prioritize the customer. By putting your customers at the heart of your strategy, you can build a loyal customer base, drive revenue growth, and achieve long-term success.