Introduction: Why CRM Marketing is Your Secret Weapon
Hey there, fellow marketers! Let’s be honest, in today’s fast-paced digital world, staying ahead of the curve feels like a constant battle. You’re juggling leads, managing customer relationships, and trying to make sense of all the data flowing your way. But what if I told you there’s a secret weapon that can simplify everything and help you achieve marketing success? That weapon is Customer Relationship Management (CRM) marketing.
CRM marketing isn’t just about software; it’s a strategic approach. It’s about understanding your customers, personalizing their experiences, and building lasting relationships. And the best part? It’s incredibly effective. In this comprehensive guide, we’ll dive deep into the world of CRM marketing and explore over 50 blog ideas to fuel your content strategy and help you dominate your niche. Get ready to transform your marketing efforts and watch your business thrive!
Part 1: Understanding the Fundamentals of CRM Marketing
1. What is CRM Marketing? A Beginner’s Guide
Let’s start with the basics. CRM marketing is the practice of using CRM software and strategies to manage and analyze customer interactions and data throughout the customer lifecycle. It’s about using technology to understand your customers better, personalize your marketing efforts, and ultimately, drive sales and loyalty. Think of it as the ultimate customer-centric approach.
2. The Benefits of CRM Marketing: Why You Need It
Why bother with CRM marketing? Because it works! Here are some key benefits:
- Improved Customer Relationships: CRM helps you understand your customers’ needs and preferences, leading to stronger relationships.
- Increased Sales: By targeting the right customers with the right messages, you can boost sales and revenue.
- Enhanced Customer Retention: Happy customers are loyal customers. CRM helps you keep them happy.
- Greater Efficiency: Automate tasks and streamline your workflow for increased productivity.
- Better Data Analysis: Gain valuable insights into customer behavior and marketing performance.
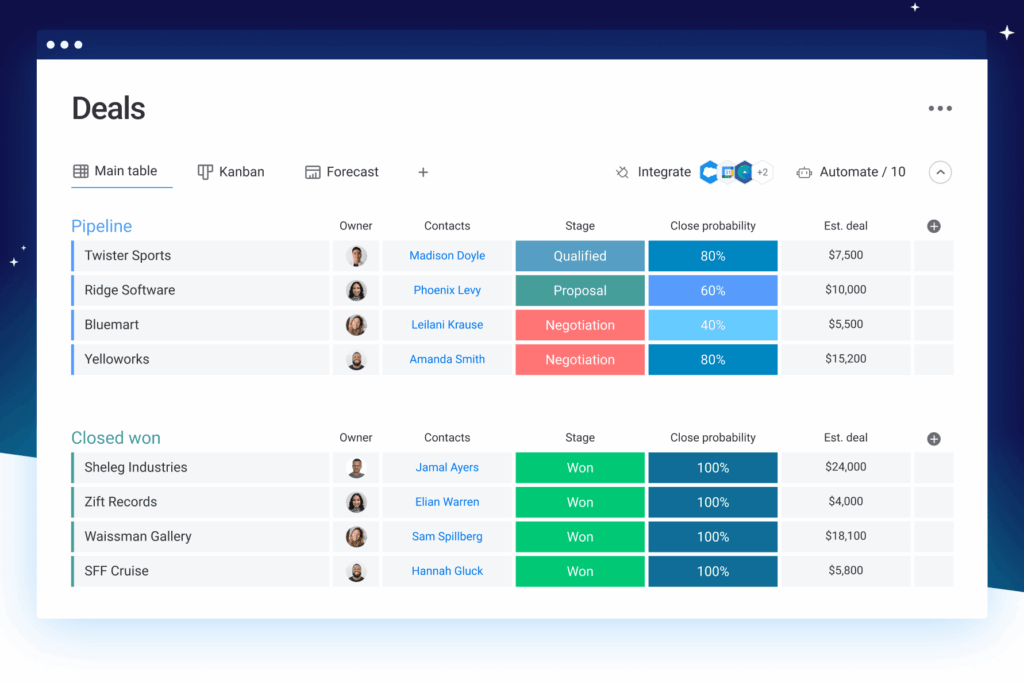
3. Key Components of a CRM System
A robust CRM system typically includes these core components:
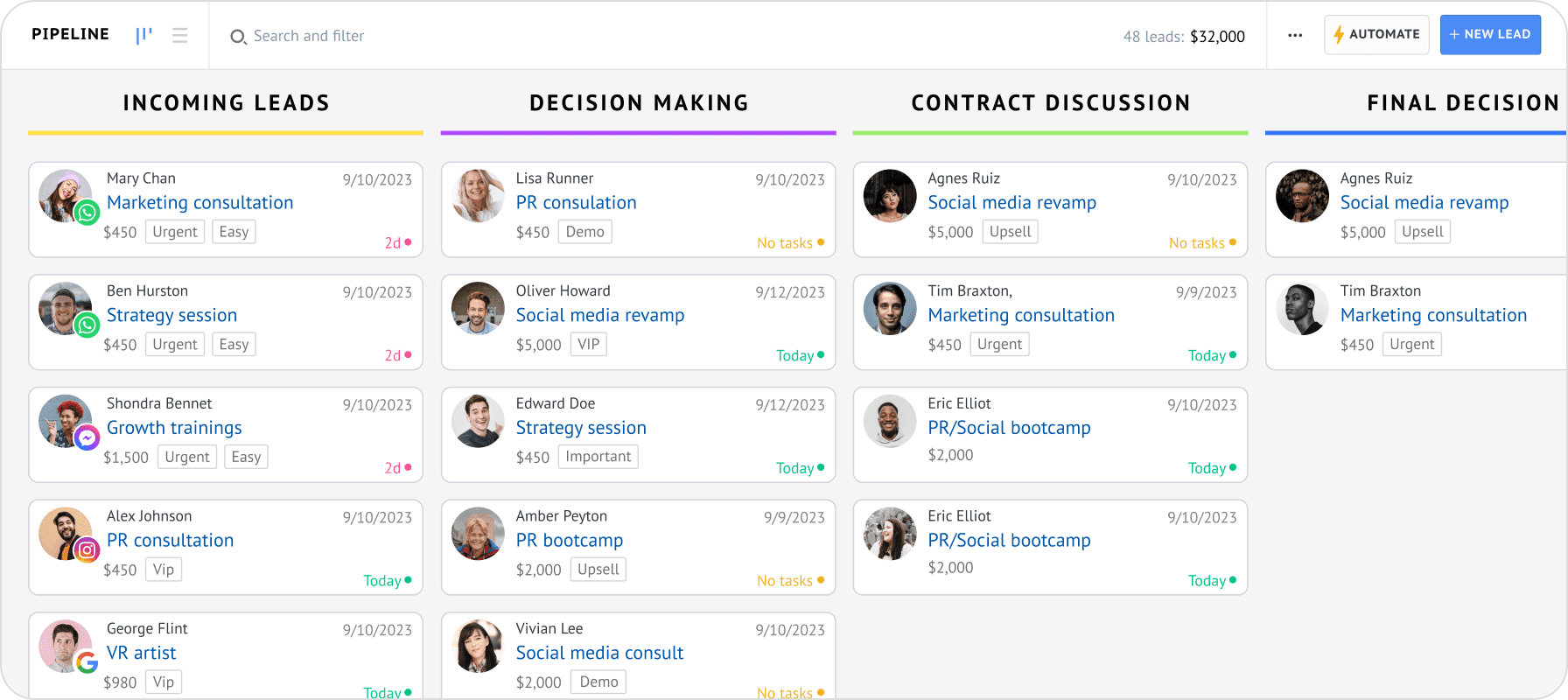
- Contact Management: Store and manage customer information.
- Sales Automation: Automate sales processes and tasks.
- Marketing Automation: Automate marketing campaigns and workflows.
- Customer Service: Manage customer support interactions.
- Analytics and Reporting: Track key metrics and gain insights.
4. Choosing the Right CRM Software: Factors to Consider
Selecting the right CRM software is crucial. Consider these factors:
- Your Business Needs: What features do you need?
- Scalability: Can the software grow with your business?
- Integration: Does it integrate with your existing tools?
- Ease of Use: Is it user-friendly for your team?
- Cost: What’s your budget?
5. CRM vs. Other Marketing Tools: Understanding the Differences
CRM is not the same as marketing automation or email marketing platforms. CRM focuses on the entire customer lifecycle, while other tools may have a more specific focus. Understanding the differences will help you integrate these tools effectively.
Part 2: Blog Ideas for CRM Marketing Strategy
6. How to Develop a CRM Marketing Strategy: A Step-by-Step Guide
Create a detailed guide on how to create a CRM marketing strategy. This should include setting goals, identifying your target audience, mapping the customer journey, and selecting the right CRM software. Provide practical tips and templates.
7. Defining Your CRM Marketing Goals: Setting KPIs for Success
Help readers understand how to define clear and measurable goals for their CRM marketing efforts. Discuss key performance indicators (KPIs) like customer acquisition cost (CAC), customer lifetime value (CLTV), and customer retention rate.
8. Segmenting Your Audience for Targeted CRM Marketing
Explain the importance of audience segmentation. Discuss various segmentation methods (demographics, psychographics, behavior) and how to use them to personalize marketing messages.
9. Mapping the Customer Journey: Understanding the Customer Lifecycle
Guide readers on how to map the customer journey, from awareness to purchase to loyalty. Show them how to identify touchpoints and optimize interactions at each stage.
10. Integrating CRM with Your Marketing Automation Platform
Show how to connect CRM with marketing automation tools to streamline processes. Discuss how to trigger automated email campaigns, personalize website content, and nurture leads.
11. Personalizing the Customer Experience with CRM
Highlight the importance of personalization. Explain how to use CRM data to create tailored content, offers, and recommendations.
12. CRM and Lead Scoring: Identifying High-Quality Leads
Teach readers how to use lead scoring to prioritize leads based on their behavior and engagement. Explain how to automate lead nurturing processes.
13. Creating Effective CRM-Driven Email Marketing Campaigns
Provide tips on creating high-converting email campaigns using CRM data. Discuss segmentation, personalization, and automation.
14. CRM for Customer Retention: Strategies to Keep Customers Loyal
Share strategies for using CRM to improve customer retention, such as personalized offers, proactive customer service, and loyalty programs.
15. Using CRM to Improve Customer Service and Support
Explain how to use CRM to manage customer service interactions, track issues, and resolve problems efficiently. Discuss the importance of providing excellent customer support.
16. A/B Testing Your CRM Marketing Efforts: Optimizing for Results
Guide readers on how to A/B test different elements of their CRM marketing campaigns, such as subject lines, email content, and landing pages.
17. Measuring the ROI of Your CRM Marketing: Tracking Key Metrics
Show readers how to measure the return on investment (ROI) of their CRM marketing efforts. Discuss key metrics and reporting tools.
18. CRM and Social Media Marketing: Integrating Your Efforts
Explain how to integrate CRM with social media platforms to manage social interactions, track customer sentiment, and run targeted ad campaigns.
Part 3: Content Ideas for CRM Software Features and Functionality
19. Top CRM Software Features You Need to Know
Provide an overview of essential CRM features, such as contact management, sales automation, marketing automation, and reporting.
20. Contact Management: Organizing and Managing Customer Data
Discuss the importance of contact management and how CRM software helps you organize and manage customer information effectively.
21. Sales Automation: Streamlining Your Sales Process
Explain how sales automation features can help you automate tasks, track deals, and improve sales efficiency.
22. Marketing Automation: Automating Your Marketing Campaigns
Discuss how marketing automation features can help you automate email campaigns, personalize content, and nurture leads.
23. Lead Management: Capturing, Nurturing, and Qualifying Leads
Explain how CRM can help you capture, nurture, and qualify leads to improve your sales pipeline.
24. Sales Forecasting: Predicting Future Sales with CRM
Show readers how to use CRM to forecast sales and make informed business decisions.
25. Reporting and Analytics: Gaining Insights from Your Data
Discuss the importance of reporting and analytics and how CRM helps you track key metrics and gain insights into your marketing performance.
26. Mobile CRM: Accessing Your Data on the Go
Explain the benefits of mobile CRM and how it allows you to access your data and manage your business from anywhere.
27. CRM Integrations: Connecting with Your Favorite Tools
Discuss the importance of CRM integrations and how they can help you connect with your favorite tools and streamline your workflow.
28. Data Security and Privacy in CRM: Protecting Customer Information
Address the importance of data security and privacy and how to protect customer information in your CRM system.
29. Customization Options in CRM: Tailoring Your System to Your Needs
Explain how to customize your CRM system to meet your specific business needs.
30. CRM for Small Businesses: Choosing the Right Software
Provide tips for small businesses on choosing the right CRM software.
31. CRM for Enterprise Businesses: Scaling Your CRM Strategy
Provide tips for enterprise businesses on scaling their CRM strategy.
Part 4: CRM Marketing Campaign Ideas
32. Welcome Email Series: Making a Great First Impression
Guide readers on how to create a welcome email series to engage new customers and introduce them to your brand.
33. Abandoned Cart Emails: Recovering Lost Sales
Explain how to use abandoned cart emails to recover lost sales and increase revenue.
34. Personalized Product Recommendations: Boosting Sales
Show readers how to use CRM data to provide personalized product recommendations and boost sales.
35. Loyalty Program Emails: Rewarding Your Best Customers
Discuss how to use CRM to create and manage loyalty programs to reward your best customers.
36. Re-engagement Campaigns: Winning Back Inactive Customers
Explain how to use re-engagement campaigns to win back inactive customers.
37. Birthday Emails: Personalizing Your Customer Interactions
Discuss the use of birthday emails to personalize customer interactions and build relationships.
38. Anniversary Emails: Celebrating Milestones with Customers
Explain how to use anniversary emails to celebrate milestones with customers and build relationships.
39. Customer Satisfaction Surveys: Gathering Feedback and Improving
Guide readers on how to use customer satisfaction surveys to gather feedback and improve their products and services.
40. Event Invitations: Driving Attendance and Engagement
Discuss how to use CRM to send event invitations and drive attendance and engagement.
41. Product Update Emails: Keeping Customers Informed
Explain how to use product update emails to keep customers informed about new features and improvements.
42. Special Offer Emails: Driving Sales and Promoting Products
Discuss how to use special offer emails to drive sales and promote products.
43. Cross-Selling and Upselling Campaigns: Increasing Revenue
Show readers how to use CRM to create cross-selling and upselling campaigns to increase revenue.
44. Win-Back Campaigns: Re-engaging Dormant Customers
Explain how to use win-back campaigns to re-engage dormant customers and increase sales.
Part 5: CRM Marketing Best Practices and Tips
45. Data Hygiene: Keeping Your CRM Data Clean and Accurate
Emphasize the importance of data hygiene and provide tips for keeping your CRM data clean and accurate.
46. Training Your Team on CRM: Maximizing Adoption
Discuss the importance of training your team on CRM and provide tips for maximizing adoption.
47. Integrating CRM with Your Website: Capturing Leads and Data
Explain how to integrate CRM with your website to capture leads and data.
48. Measuring and Analyzing CRM Performance: Tracking Your Success
Discuss the importance of measuring and analyzing CRM performance and provide tips for tracking your success.
49. Staying Up-to-Date with CRM Trends: Continuous Learning
Encourage readers to stay up-to-date with CRM trends and continuously learn to improve their marketing efforts.
50. Common CRM Mistakes to Avoid
Highlight common CRM mistakes and how to avoid them.
51. Future of CRM Marketing: Trends to Watch
Discuss emerging trends in CRM marketing, such as AI-powered CRM, and the rise of customer data platforms (CDPs).
52. Case Studies: CRM Marketing Success Stories
Include examples of real-world CRM marketing success stories to inspire readers.
Conclusion: Embrace the Power of CRM Marketing
So there you have it! Over 50 blog ideas to help you supercharge your CRM marketing efforts. Remember, CRM marketing is not a one-size-fits-all solution. It requires careful planning, execution, and continuous optimization. By implementing these ideas and staying focused on your customers, you can build stronger relationships, drive more sales, and achieve lasting success. Now go forth and conquer the world of CRM marketing!
If you’re looking for more insights into the dynamic world of marketing, don’t hesitate to explore other articles on our blog. We regularly update with fresh content, valuable tips, and the latest trends to keep you ahead of the curve. Remember, the path to marketing mastery is paved with continuous learning and adaptation. Embrace the challenges, celebrate the successes, and never stop exploring the endless possibilities that CRM marketing offers. Happy marketing!