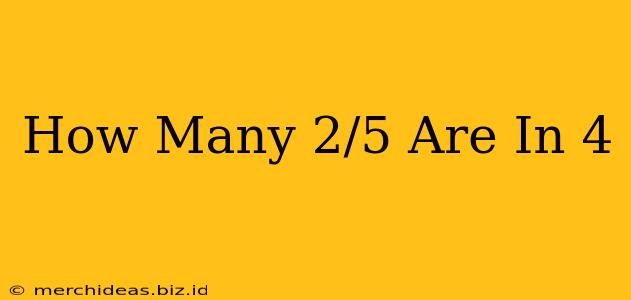How Many 2/5 Are in 4? A Step-by-Step Guide to Solving Fraction Division Problems
This seemingly simple question, "How many 2/5 are in 4?", actually touches on a fundamental math concept: fraction division. Understanding this concept is crucial for various applications, from baking (measuring ingredients) to construction (calculating materials). Let's break it down step-by-step.
Understanding the Problem:
The question is essentially asking: "How many times does 2/5 go into 4?" This translates to a division problem: 4 ÷ (2/5).
Method 1: Converting to Improper Fractions
This is a common and straightforward method. First, we convert the whole number 4 into an improper fraction. Remember, any whole number can be written as a fraction with a denominator of 1.
-
Step 1: Rewrite 4 as 4/1. This represents four whole units.
-
Step 2: Invert the second fraction (reciprocal). The reciprocal of 2/5 is 5/2.
-
Step 3: Change the division sign to a multiplication sign. Now our problem looks like this: (4/1) x (5/2)
-
Step 4: Multiply the numerators and the denominators. (4 x 5) / (1 x 2) = 20/2
-
Step 5: Simplify the resulting fraction. 20/2 simplifies to 10.
Therefore, there are 10 instances of 2/5 in 4.
Method 2: Visual Representation
Sometimes, a visual approach helps solidify understanding. Imagine you have four whole pies. Each pie is divided into fifths. How many pieces of size 2/5 can you get?
-
Step 1: Divide each pie into fifths. You now have 20 pieces (4 pies x 5 pieces/pie).
-
Step 2: Group the pieces into sets of 2/5. Each set consists of two fifths.
-
Step 3: Count the sets. You'll find you have 10 sets of 2/5.
This visual confirms our answer: there are 10 instances of 2/5 in 4.
Method 3: Using Decimal Equivalents
You could also solve this by converting the fraction to a decimal and then dividing.
-
Step 1: Convert 2/5 to a decimal: 2/5 = 0.4
-
Step 2: Divide 4 by 0.4: 4 ÷ 0.4 = 10
Again, we arrive at the answer: 10.
Conclusion:
No matter which method you use, the answer remains the same: there are 10 instances of 2/5 in 4. Mastering fraction division is a valuable skill, and understanding these different approaches will help you tackle similar problems with confidence. Remember to practice regularly to build your proficiency!